mjtc
GF Platina
- Entrou
- Fev 10, 2010
- Mensagens
- 9,475
- Gostos Recebidos
- 11
Existem óptimos professores de ciência no mundo, é claro. Mas para atingir a máxima compreensão, nada se compara ao poder de uma imagem.
1. Isso é um triângulo de Reuleaux

Um triângulo de Reuleaux não é propriamente um triângulo, mas sim uma
curva de largura constante que pode ser formada a partir de triângulos
equilateros e esferas. Por outras palavras, é uma forma plana convexa cuja
largura é a mesma independentemente da orientação da curva.
2. As curvas de largura constante podem fazer furos quadrados.
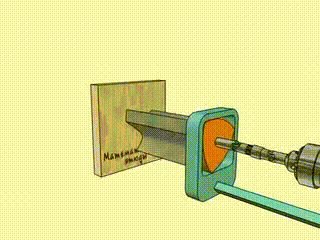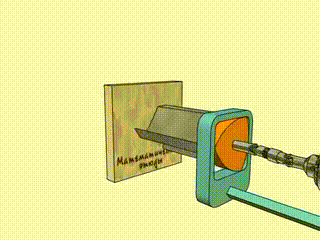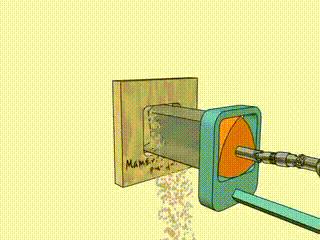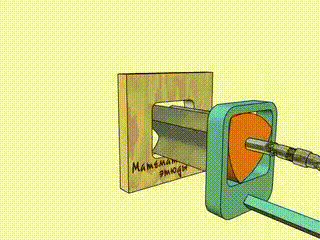
3. É por isso que Pi é significativo.

Essa animação mostra o acto de desenrolar (ou tentar desenrolar) a circunferência de um círculo, ilustrando a razão de π.
4. Como fazer o Triângulo de Pascal.

Esses triângulos são utilizados em álgebra
e probabilidade, por exemplo, para encontrar
combinações.
5. Este é o método de dobra Miura.

É um método de dobragem de uma superfície plana
para chegar a um volume menor. É usado nos painéis
solares de satélites.
6. Isso é um radiano

O radiano é a unidade padrão de medida angular usada em muitas áreas
da matemática.
7. Isso é uma matriz transposta.

A matriz transposta é formada ao
inverter a ordem de uma matriz,
trocando os elementos das linhas
pelo das colunas e vice-versa. Dada
uma matriz A, sua matriz transposta
será representada por At.
8. Este é um Triângulo de Sierpinski

Esse triângulo é uma espécie de
fractal, um padrão matematicamente
gerado que pode ser reproduzido em
qualquer ampliação ou redução.
9. É assim que se convertem coordenadas cartesianas em coordenadas polares.

10. Isso são ângulos exteriores de polígonos. Eles somam 360 graus.

1. Isso é um triângulo de Reuleaux

Um triângulo de Reuleaux não é propriamente um triângulo, mas sim uma
curva de largura constante que pode ser formada a partir de triângulos
equilateros e esferas. Por outras palavras, é uma forma plana convexa cuja
largura é a mesma independentemente da orientação da curva.
2. As curvas de largura constante podem fazer furos quadrados.

3. É por isso que Pi é significativo.

Essa animação mostra o acto de desenrolar (ou tentar desenrolar) a circunferência de um círculo, ilustrando a razão de π.
4. Como fazer o Triângulo de Pascal.

Esses triângulos são utilizados em álgebra
e probabilidade, por exemplo, para encontrar
combinações.
5. Este é o método de dobra Miura.

É um método de dobragem de uma superfície plana
para chegar a um volume menor. É usado nos painéis
solares de satélites.
6. Isso é um radiano

O radiano é a unidade padrão de medida angular usada em muitas áreas
da matemática.
7. Isso é uma matriz transposta.

A matriz transposta é formada ao
inverter a ordem de uma matriz,
trocando os elementos das linhas
pelo das colunas e vice-versa. Dada
uma matriz A, sua matriz transposta
será representada por At.
8. Este é um Triângulo de Sierpinski

Esse triângulo é uma espécie de
fractal, um padrão matematicamente
gerado que pode ser reproduzido em
qualquer ampliação ou redução.
9. É assim que se convertem coordenadas cartesianas em coordenadas polares.

10. Isso são ângulos exteriores de polígonos. Eles somam 360 graus.

Última edição:












